Introduction to Econometrics - Matrix Algebra

What follows under this section, is an introduction to matrix algebra which is essential in order to understand the discussion of more advanced econometrics and statistics. Most properties are only defined or described without giving examples, exercises, or rigorous proofs. In any case remember, mathematics is pure fun!

We write a column and row vector as follows

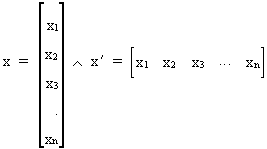
(I.IV-1)

where the prime (') is an indication of transposition.

The length of a vector is defined as

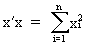
(I.IV-2)

Note the following, obvious relationships

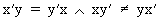
(I.IV-3)

We write a n*m matrix as follows

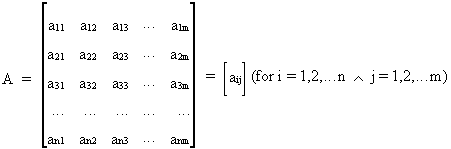
(I.IV-4)

Addition of matrices can be defined as

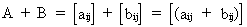
(I.IV-5)

whereas multiplication can be written as

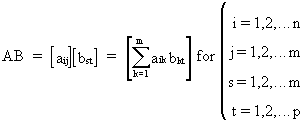
(I.IV-6)

Transposition of matrices has two simple properties

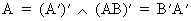
(I.IV-7)

The multiplication of two diagonal matrices results in a diagonal matrix

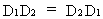
(I.IV-8)

where a 'diagonal matrix' can be defined as

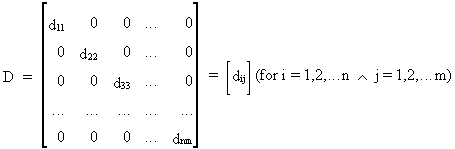
(I.IV-9)

A special diagonal matrix is a matrix where all diagonal elements are equal to one (identity matrix denoted I). Therefore, it is obvious that

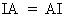
(I.IV-10)

A matrix with only zero elements is neutral in addition

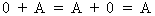
(I.IV-11)

Vectors are told to be linearly independent if

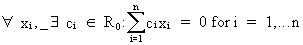
(I.IV-12)

Now we are able to define the rank of a matrix as the number of linearly independent rows or columns. Also note that all zero matrices have rank = 0. The rank of a (m*n) matrix is equal to the rank of the largest sub matrix with a determinant different from zero where the determinant of a matrix is defined by

Note that a determinant of a two by two matrix can be found by

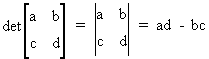
(I.IV-13)

It is also quite obvious that the rank of a product of two matrices is less or equal to the rank of either the one or the other matrix.

Transposition does not alter the rank of a matrix.

If a square matrix has a full rank (rank equal to the number of rows or columns) we call this matrix not singular.

Furthermore, if we have a square non singular matrix then the inverse of a matrix A can be defined as

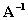
if and only if

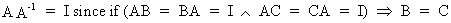
(I.IV-14)

The inverse of an inverse matrix, is equal to the original matrix

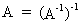
(I.IV-15)

and the inverse of the transposed is the transposition of the inverse matrix

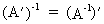
(I.IV-16)

A diagonal matrix is non singular if, and only if all diagonal elements are different from zero. Above this, the inverse of such a matrix can be found by writing a diagonal matrix where all diagonal elements are replaced by their respective reciprocals.

The determinant of a product AB (if AB exists) is equal to the product of the determinants if both matrices are square

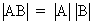
(I.IV-17)

The rank of AB and the rank of CA are equal to the rank of A if B and C are non singular.

If A and B are of the same order then

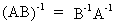
(I.IV-18)

If

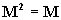
then M is said to be idempotent. In our discussions we'll also always assume that these idempotent matrices are symmetric (which means that the element of the i-th row and the j-th column is equal to the element of the j-th row and the i-th column).

An important example of an idempotent matrix is

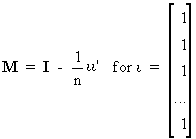
(I.IV-19)

which can be shown quite easily

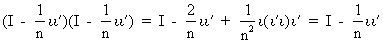
(I.IV-20)

Idempotent matrices are very important in order to write variables as deviations from the mean. For instance, if B is an observation matrix and M is the idempotent matrix of (I.IV-20), then we can write

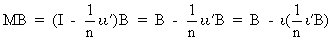
(I.IV-21)

where obviously all columns of B have been written as their deviation from the mean.

Even the sum of the square products B'B of a square matrix B can be written as deviations from the mean: (MB)'MB = B'MB (where M is again idempotent).

When using two different matrices B and C it is still possible to write the deviations from the mean of the sum of square products (B'C) as follows: (MB)'MC = B'MC.

Define the trace of a square matrix A as

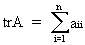
(I.IV-22)

It is obvious that the following rules hold for the trace of a matrix:

a) tr (k A) = k tr A where k is a real number

b) tr(A+B) = tr A + tr B

c) tr (AB) = tr (BA)

d) tr A = rank A if A is idempotent

A quadratic form associated with a symmetric square matrix A is defined as the scalar

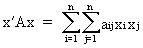
(I.IV-23)

(A is considered to be a square symmetric matrix).

A is called a positive definite matrix if and only if

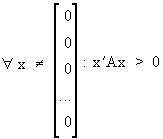
(I.IV-24)

A positive semi definite matrix is

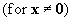
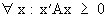
(I.IV-25)

Obviously a negative definite and a negative semi definite matrix can be defined analogously.

An indefinite matrix however is defined

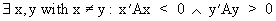
(I.IV-26)

The matrix A is positive definite if

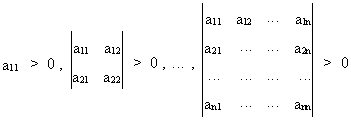
(I.IV-27)

All principal minors and the determinant of a matrix A are positive if A is positive definite.

A very important property is that all positive definite matrices are non singular!

If A is positive definite (pos. semi def.) and B is non singular then B'AB is also positive definite (pos. semi def.).

If there exists a m*n matrix A with rank m<n then AA' is positive definite and A'A is positive semi definite but never positive definite.

If there exists a m*n matrix A with rank r<m and r<n then AA' and A'A are both positive semi definite but neither will be positive definite.

If there exists a square symmetric and positive definite matrix A then there always exists a non singular matrix P such that P'P = A. This is a very important property.

Define an eigenvalue lambda and an eigenvector x of the square matrix A as

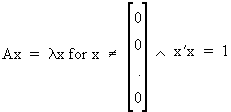
(I.IV-28)

Since the eigenvector x is different from the zero vector the following is valid

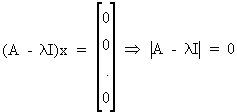
(I.IV-29)

Note that eigenvectors are also called the "latent" roots.

It is very interesting to note that

(I.IV-30)

If we define the complex (imaginary) number i such that

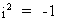
(I.IV-31)

then the latent root (x + iy) of a symmetric square matrix A is always real! Proof:

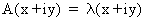
(I.IV-32)

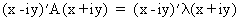
(I.IV-33)

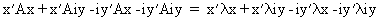
(I.IV-34)

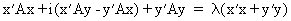
(I.IV-35)

Since, due to the symmetry of A,

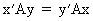
(I.IV-36)

it follows from (I.IV-35) and (I.IV-36) that

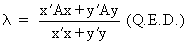
(I.IV-37)

If a square matrix A is symmetric then the eigenvectors corresponding to the different eigenvalues are all orthogonal (independent from each other). Suppose we would have two latent roots with corresponding eigenvectors x and y then we can write

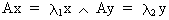
(I.IV-38)

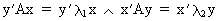
(I.IV-39)

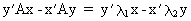
(I.IV-40)

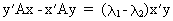
(I.IV-41)

and since

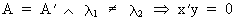
(I.IV-42)

which implies that the eigenvectors corresponding to different eigenvalues are independent.

If x is a characteristic (eigen)vector of the square matrix A with root lambda then

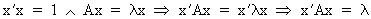
(I.IV-43)

If x is an eigenvector of A then -x is also an eigenvector of this matrix. Note the following (almost trivial) relationship

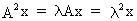
(I.IV-44)

If A is a non singular square matrix then the roots of the inverse of A are equal to the reciprocal values of the roots of A but the eigenvectors are the same. This can be seen quite easily by

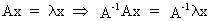
(I.IV-45)

and therefore

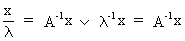
(I.IV-46)

The latent roots of a positive definite (pos. semi def.) matrix are positive (non negative). Of course, analogously one can formulate a similar property for negative (semi) definite matrices.

The number of roots of a symmetric matrix A that are different from zero is equal to the rank of A.

If all roots of a symmetric matrix A are positive (non negative) then all the diagonal elements of A are positive (non negative).

The non zero roots of AA' and A'A are always the same.

If x₁, x₂ are eigenvectors (corresponding to different roots) of AA' are pair wise independent with unit length, then the vectors A'x₁, A'x₂ are also orthogonal but without unit length (except if all l values are equal to one).

Define an orthogonal matrix A as

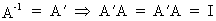
(I.IV-47)

which also implies that all rows and columns have unit length.

If A is a square matrix with different roots and corresponding eigenvectors

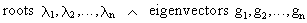
(I.IV-48)

then it follows by definition (I.IV-28) that

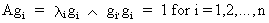
(I.IV-49)

and

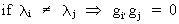
(I.IV-50)

Now we put the orthogonal vectors g_i into a n*n matrix G like

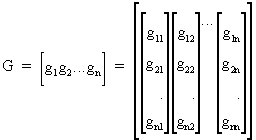
(I.IV-51)

and therefore it follows that G'G = I (and thus G is orthogonal). Furthermore, by pre-multiplying G by matrix A, we obtain

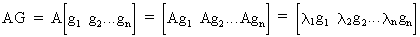
(I.IV-52)

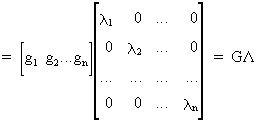
(I.IV-53)

Now we can easily find that

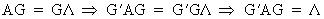
(I.IV-54)

and

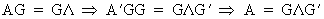
(I.IV-55)

If a matrix A has rank r then there are only r non zero eigenvectors (with rank 1) and n-r zero eigenvectors (abstraction has been made for the sign).

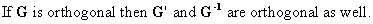
The determinant of an orthogonal matrix is equal to 1 or -1.

The real roots of an orthogonal matrix G are always equal to 1 or -1 which can be seen quite easily

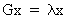
(I.IV-56)

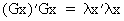
(I.IV-57)

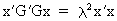
(I.IV-58)

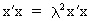
(I.IV-59)

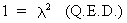
(I.IV-60)

If A is a positive semi definite matrix of rank r then

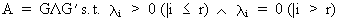
(I.IV-61)

therefore P' is equal to

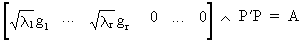
(I.IV-62)

All idempotent matrices have a root of 0 or 1.

For the square idempotent matrix M with rank r the following property is valid

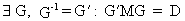
(I.IV-63)

where D is a diagonal matrix with r diagonal elements equal to 1 (and all other elements equal to zero).

All idempotent matrices A are positive semi definite with non negative diagonal elements since

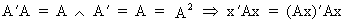
(I.IV-64)

which is just a sum of squares of the elements of Ax.

If a square idempotent matrix A is non singular then A must be equal to the identity matrix I since

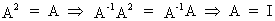
(I.IV-65)

If A is idempotent and G is orthogonal then G'AG is idempotent as well since

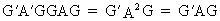
(I.IV-66)

If A is idempotent then I - A is also idempotent but A(I - A) = O.

If A is idempotent and the element a_ij = 0 then it follows that the i-th row vector and the j-th column vector consists of nothing but zero elements.

We define the following derivatives of matrices (where A is not necessarily symmetric)

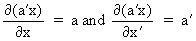
(I.IV-67)

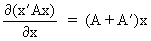
(I.IV-68)

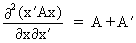
(I.IV-69)

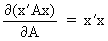
(I.IV-70)

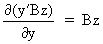
(I.IV-71)

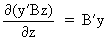
(I.IV-72)

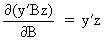
(I.IV-73)

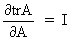
(I.IV-74)

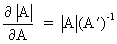
(I.IV-75)

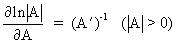
(I.IV-76)

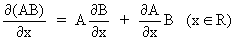
(I.IV-77)

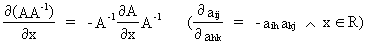
(I.IV-78)

We define the Kronecker (or Tensor) product as

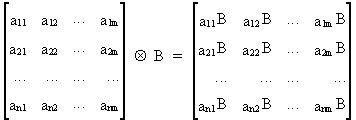
(I.IV-79)

with the following properties

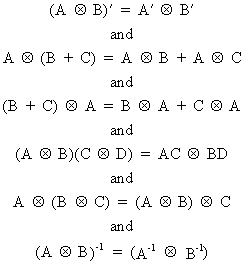
(I.IV-80)

and last but not least

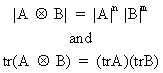
(I.IV-81)

where A is a n*n, and B is a m*m matrix.

Sometimes it is useful to write matrix expressions in partitioned form. Addition and multiplication rules with respect to partitioned matrices are quite simple

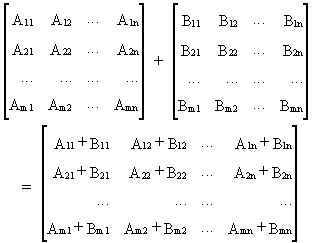
(I.IV-82)

and

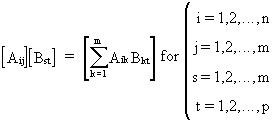
(I.IV-83)

which is a generalization of (I.IV-6) and for which A_ik has the same number of columns as the number of rows of B_kt.

It is easily verified that the inverse of a symmetric partitioned matrix can be written as

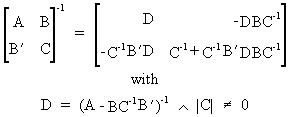
(I.IV-84)

or equivalently

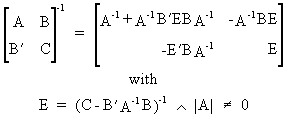
(I.IV-85)

Sometimes a matrix is written in upper or lower triangular form. An upper triangular matrix A(m*n) is a matrix were all elements (for m larger than n) are zero. Analogously a lower triangular matrix can be defined.

Imagine an upper triangular matrix T(3*3) with units in the diagonal, and a diagonal matrix D(3*3)

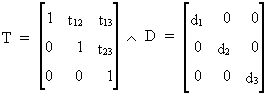
(I.IV-86)

then

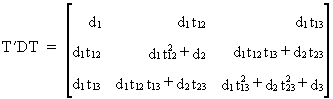
(I.IV-87)

It can be shown that any matrix square symmetric A can be written as T'DT according to Choleski's decomp. theorem. It is also interesting to see that the A matrix can be transformed to become a diagonal matrix:

D = (T')^-1AT.